| Also, read |
| Basics of Trigonometry |
| Trigonometry for class 10 |
| Trigonometric Formulas |
| Inverse Trigonometric Function |
Applications of Trigonometry:
Trigonometry mainly deals with measurements of length, angle, height of any body of this universe, as a part of mathematics. Basically, trigonometry in ancient time was developed to read astronomy, geography and related topics but as modernization of study began mathematician and scientists started using it as a part of mathematics, physics as well as engineering subjects. Calculus in Mathematics uses application of trigonometry most which occupy the most important portion in mathematics, also statics and algebra use it.
One had not enough knowledge of trigonometry is still thinking about “is there exist a measurement scale of such length that they can measure the distance between Earth and Mars. And one person holding the scale on earth and other at Mars?” (jokes apart).
The answer to this question is “absolutely not”. There is application of trigonometry to calculate that distance by having some known quantities.
Let’s first know what trigonometry actually is?
Trigonometry is mainly the relationship between different components of triangle as length, angle, inclination, height etc. Further, it deals in application of trigonometry. Trigonometry is only applicable for right triangle. But measurement can be done for every triangle with it. As every triangle can be reduced to two right triangles by drawing perpendicular to opposite sides from any vertex.
Applications of Trigonometry:
By the use of trigonometry, every type of measurement can be easy in dealing with. In class 10 we read about application of trigonometry as a separate chapter.
Look at the picture

There are some common terms used in applications of trigonometry which we discuss in this section.
Line of sight: Suppose, you are the observer and you are seeing the parrot on large electric pole. The distance between your eyes and that parrot is called Line of sight.
Angle of Elevation: As the word elevation itself mean upward move. This is the angle between the straight line from your eye on the pole horizontally and the line of sight of parrot.
To remember this angle simply learn as the angle from down to up move.
Angle of Depression: As the word depression mean lagging down. When you are standing on roof of your house you show a football lying on the ground. The angle between the horizontal line from your eye and the line of sight of football is angle of depression.
Application of trigonometry in real world:
In modern days science is developing rapidly. Almost in every field the requirement of trigonometry is increasing. You will amaze to know that the music which you often listen also uses trigonometry.
List of fields where application of trigonometry is involved:
- Astronomy and Geography which uses spherical Trigonometry.
- Navigation
- Digital Games
- Marine Subliving
- Engineering
- Flight engineering
- Marine engineering
- Communication engineering
- Aviation body
- Industries
- Arms industry
- Naval industry
- Vehicle industries
- Satellite
- Maps making i.e. cartography
- Building construction
- Measurement of height of mountains
Examples related to application of trigonometry:
1. An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
Solution:PD
Here, AB is the chimney, CD the observer and angle ADE is the angle of elevation. In this case, ADE is a triangle, right-angled at E and we are have to find the height of the chimney.
We have AB = AE + BE = AE + 1.5
and DE = CB = 28.5 m
To determine AE, we choose a trigonometric ratio, which involves both AE and DE. Let us choose the tangent of the angle of elevation.
Now, tan 45° = \(\frac{AE}{DE}\)
i.e., 1 =\(\frac{AE}{28.5}\)
Therefore, AE = 28.5
So the height of the chimney (AB) = (28.5 + 1.5) m = 30 m.
2. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Solution:
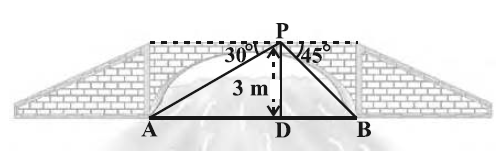
A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e., DP = 3 m. We are interested to determine the width of the river, which is the length of the side AB of the triangle APB.
AB = AD + DB
In right triangle APD,
angle A = 30°.
Tan 30° = \(\frac{PD}{AD}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{3}{AD}\)
AD = 3\(\sqrt{3}\) m
Also, in right triangle PBD,
angle B = 45°. So, BD = PD = 3 m
AB = BD + AD = 3 + 3\(\sqrt{3}\)
Therefore, width of river in question is 3(1 + \(\sqrt{3}\))









Be First to Comment