| Triangle: Definition and Formula |
| Properties of triangle |
| Triangle: For class 9 |
| Triangle For class 10 |
| Heron’s Formula |
Area of Parallelograms and triangles:
In the present scenario, we see there is enormous use of area, especially of parallelogram and triangles. When we see around, we find that either it is a building, a garden, roads, plots or items of furniture, all these things while making involves the measurement of area.
Area
Area is simply the measurement of magnitude of planar region enclosed within a defined closed figure. It is always measured in square units.
However, three types of parallelograms are there:
- Rectangle
- Rhombus
- Square
- Area of rectangle = length x breadth
- The area of rhombus = \(\frac{1}{2}\) d1 x d2
- Area of square = (side)2
Area of congruent figures:
Two figures are said to be congruent if they have same shape and size. As we have provided details about congruency in last section please read it for better understanding.
“If two figures are congruent then their area must be equal.”
However, the converse of the same may not be true. i.e.
“If area of two figures are equal then they may or may not be congruent.”
Area of two different joined figures:
When two different figures are joined end to end making a single big figure then the area of big figure is equal to the sum of the two joined small figures.
If O is the big figure joined by two small figures A and B then their area will be
ar(O) = ar(A) + ar(B)

Figures on the same base and between same parallels:
The two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the rest vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.

In fig. 1. Trapezium ABCD and parallelogram EFCD are on the same base DC and between the same parallels DC and AF.
Fig. 2. Also, parallelograms PQRS and MNRS are on the same base SR and between the same parallels SR and PN.
In fig. 3. In the same way, triangles ABC and DBC lie on the same base BC and between the same parallels BC and AD.
Area of parallelogram:
The area of parallelogram is given by
“Area ||gm = Base of parallelogram X altitude from the base”
Parallelograms on the same base and between same parallels:
The much interesting fact about parallelogram in this condition is
“Parallelograms on the same base and between the same parallels have equal area.”
Converse is also true-
“The parallelograms on the same base and having equal areas lie between the same parallels.”
Area of parallelogram and triangle on same base and between same parallels:
“If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.”
Area of triangle:
The area of triangle is given by-
“Area (∆) = ½ base x height”
Triangle on the same base and between the same parallels:
“The two triangles which have a common base and lie between the same parallels have equal areas.”
Converse is also true-
“Triangles on the same base and having equal areas lie between the same parallels.”
Also,
“A median of a triangle divides it into two triangles of equal areas.”
Examples related to area of parallelogram and triangle:
- In the given figure, if ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ Then prove that ar (ABCD) = ar (EFCD) and ar (ABCD) = DC × AL.

Solution:
As we know that rectangle is also a parallelogram,
therefore, ar (ABCD) = ar (EFCD)
From above result,
ar (ABCD) = DC × FC (Area of the rectangle = length × breadth) (1)
As AL ⊥ DC, therefore, AFCL is also a rectangle
So, AL = FC (2)
Therefore, ar (ABCD) = DC × AL [From (1) and (2)]
- Show that a median of a triangle divides it into two triangles of equal areas.
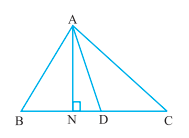
Solution:
Let ABC be a triangle and let AD be one of its medians
We have to show that
ar (ABD) = ar (ACD).
Since the formula for area involves altitude, let us
draw AN ⊥ BC.
Now ar(ABD) = ½ × base × altitude (of ∆ ABD)
= \(\frac{1}{2}\) × BD × AN
= \(\frac{1}{2}\) × CD × AN (As BD = CD)
= \(\frac{1}{2}\) × base × altitude (of ∆ACD)
= ar(∆ACD)











Be First to Comment