Light Reflection and Refraction, Class 10 Notes

Light Reflection and Reflection:

• Light is a form of energy which gives us sensation of vision.
• Light itself is invisible but makes the thing visible.
• Visible light is electromagnetic radiation belongs to a particular part of electromagnetic spectrum.
• The object which has its own light is said to be luminous object. Ex: sun, lamp, bulb etc.
• In our day to day life, we see several phenomena associated with light i.e. twinkling of stars, image formation, rainbow colours etc.
• In this article, we will read light reflection and refraction, which is an important chapter for class 10.

Properties of light:

• Light is an electromagnetic wave so it doesn’t require any material medium for travel.
• It possess both particle as well as wave
• Light takes straight path for their travel.
• It also causes shadow formation.
• The speed of light is 3,00,000 kilometres per second.
• Colour phenomena is also caused by the presence of light.
• Reflection, refraction and absorption are observed in case of incidence of light on any surface.
• Ray of light is the line drawn in the direction of propagation of light.
• The beam of light is the bundle or group of rays emitted from a source together.

There are three types of beam of light:

1. Convergent beam: A group of rays of light meeting at a common point.
2. Divergent beam: The spreading out of light rays emitted from a source.
3. Parallel beam: A bundle of rays of light parallel to each other.

Reflection of light:

• When light gets incident on any surface and changes its direction to the same medium then this phenomenon is called reflection of light.
• If the surface is smooth and shiny, the light will reflect at the same angle as it hit the surface.
• We follow the rules of light reflection and refraction for class 10 notes.

Laws of reflection of light:

There are two laws of reflection. These laws are applicable for all types of reflecting surfaces. They are:

• The angle of incidence is always equal to the angle of reflection. i.e. ∠i = ∠r
• The incident ray, the reflected ray and normal to the plane at the point of incidence, all lie in the same plane.

Types of mirrors:

There are two types of mirrors. They are plane and spherical mirrors.

1. Plane mirror:

A plane (flat) glass polished with silver paint on either side is said to be plane mirror. A coat of red paint is required over the silver polish to protect silver layer.

Image formation by a plane mirror:

• When two rays actually meet or appears to meet at a point then image is formed.
• A plane mirror always forms virtual and erect
• The distance of object from the mirror is same as the distance of the image of the mirror.
• Size of image and the object is same.
• A plane mirror forms laterally inverted

Real and virtual image:

Real image	Virtual image
When light rays actually meet at a point then real image is formed.	When light rays appears to meet at a point then virtual image is formed.
It can be obtained on a screen.	We can’t obtain it on screen.
Real image are always inverted.	Virtual image are always erect.

Lateral inversion:

• When left side of the object appears right in the image and vice versa is said to be lateral inversion.
• There are many uses lateral inversion. We see on Ambulance written laterally inverted and we see it actual in our side mirror.

2. Spherical mirrors:

• Any mirror which has curved reflecting surface are spherical mirrors.
• Spherical mirror is a part of a sphere.

Types of spherical mirrors:

There are two types of spherical mirrors:

Concave mirror:

• A spherical mirror whose reflecting surface is curved inwards is said to be concave mirror.
• It is also called converging mirror as it converges parallel beam of light falling on it.

Convex mirror

• A spherical mirror whose reflecting surface is curved outwards is said to be convex mirror.
• It is also called diverging mirror as it diverges parallel beam of light falling on it.

Terminology related to spherical mirrors:

To read light reflection and refraction we must be aware of some common terminology. They are:

1. Principal axis: Pole and center of curvature is joined by a line called principal axis.
2. Pole: The center of the mirror is pole. We denote it by ‘P’.
3. Aperture: The effective length of the mirror is aperture.
4. Center of curvature: The center of the sphere which mirror is a part is center of curvature. It is denoted by ‘C’.
5. Radius of curvature: The radius of the sphere which mirror is a part is radius of curvature.
6. Focus: When parallel light beam is incident on the spherical mirror, then after reflection, the point at which they meet or appears to meet is said to be focus of that mirror.
7. Focal length: The length of the line joining pole and focus of the spherical mirror is its focal length. It is denoted by the symbol ‘f’.

Ray diagram:

There are certain rules we should follow to make ray diagrams which will further used in understanding light reflection and refraction.

1. A beam of parallel rays incident on spherical mirror after reflection passes through focus. In case of concave mirror the reflected ray converges to focus but in case of convex mirror the ray appears to diverge from focus.
2. The incident ray when passes through focus after reflection it passes parallel to the principal axis.
3. A ray incident on the spherical mirror passing through center of curvature returns back on same path.
4. A ray incident to the pole of the mirror after reflection makes equal angle with the principal axis.

Images formed by concave mirror:

Here are the ray diagrams for images formed by concave mirror when object is kept at different position with respect to the concave mirror:

Position of object	Position of image	Nature of image	Size of image
At infinity	At Focus ‘F’	Real & inverted	Point sized
At far from ‘C’	between ‘F’ and ‘C’	’’	Diminished
At ‘C’	At ‘C’	’’	Same size as object
B/w ‘F’ & ‘C’	Far from ‘C’	’’	Enlarged
At Focus ‘F’	At infinity	’’	Highly enlarged
B/w ‘P’ & ‘F’	Behind the mirror	Virtual & Erect	Enlarged

Uses of concave mirror:

• It is used in search lights, vehicle headlights, torch.
• We use it as a shaving mirror.
• It is used by doctors (dentists) to see the enlarged image of the teeth.
• In solar furnace large concave mirrors are used to converge solar heat at a single point.

Images formed by convex mirror:

Position of object	Position of image	Nature of image	Size of image
At infinity	At Focus ‘F’	Virtual & Erect	Point sized
B/w pole and infinity	between ‘P’ and ‘F’	’’	Diminished

Uses of convex mirror:

• Convex mirror is used as the rear view mirror as it covers wide view and the image is always erect.
• In shops it is used as the security mirror. Now CCTV does the same.
• At danger traffic turns it is used to see the opposite comers.

Sign convention used in spherical mirror:

These observable conventions will help you in solving numerical related to light reflection and refraction.

• Object is always placed to the left of mirror.
• All distance are measured from pole of the mirror.
• Distances which are measured in the direction of incident ray are positive.
• Distances which are measured in the opposite direction of incident ray are n
• All distances measured above the principal axis along y-axis are positive.
• Distances measured below the principal axis along negative y-axis are negative.

Note: Object distance (U) is always negative, focal length of concave mirror is negative where convex mirror is positive.

Mirror formula:

The mirror formula in which v is the image distance, u is the object distance, and f is the focal length is given by:

\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)

Magnification formula:

Magnification is the ratio of height of image to that of the object. It will take each case of light reflection and refraction either in mirror or lens.

m = \(\frac{Height\:of\:image}{Height\:of\:object} = \frac{h_i}{ h_o}\)

Also, m = \(\frac{-v}{u}\)

Rules based on magnification:

• If m is negative then image is real but when it is positive then image is virtual.
• If h_i = h_o then m = 1, i.e. image is equal to the object, if h_i > h_o then m >1 image is enlarged also if h_i < h_o then m<1 image is diminished.
• Magnification of plane mirror is always +1.
• If m is +ve and less than 1 then it is convex mirror.
• If m is +ve and more than 1 also when m<1 then it is concave mirror.

Refraction:

The bending of light when it passes from one medium to other is said to be refraction of light.

By this we can distinguish light reflection and refraction.

Glass slab experiment:

• When there is one different medium (glass slab) between two same medium and the light bending will be parallel to the incident ray.
• The distance between these two lines are called lateral displacement.
• Lateral displacement depends upon thickness and refractive index of the glass slab.

Laws of refraction:

• The incident ray, the refracted ray and normal to the interface of two transparent media at the point of incidence all lies in the same plane.
• The ratio of sine of angle of incidence to the sine of angle of refraction is always constant, for a light of given colour and for a given media. This law is also called Snell’s law.
  \(\frac{sin θ_1}{sin θ_2} = constant\)

Refractive index:

• The ratio of speed of light in given pair of media is said to be refractive index of one medium with respect to the other.
• It is denoted by ‘n’.
• n₂₁ = \(\frac{velocity\:of\:light\:in\:medium\:1}{velocity\:of\:light\:in\:medium\:2}\) it means refractive index of 2 with respect to 1.
• Refractive index of one medium with respect to vaccum or air is called absolute refractive index.
• n₁₂ = \(\frac{1}{n_{21}}\)  i.e. refractive index of one medium is reciprocal of the other.
• Refractive index of diamond is 42 which is highest till date.
• Among two media if refractive index of one medium is higher than the other then medium 1 is called optically denser medium.
• Among two media if refractive index of one medium is less than the other then medium 1 is called optically rarer medium.
• When light enters from optically rarer to denser medium it bends towards the normal.
• When light travels from optically denser to rarer medium then it bends away from the normal.

Spherical Lens:

• A lens whose surface is a part of sphere is said to be spherical lens.
• Simply, a lens whose both surfaces are curved is spherical lens.
• There are two types of lens the first one is concave lens and the other one is convex lens.

Image formation by convex lens:

There are some conditions which we should follow while making ray diagram of image formation by convex lens:

1. If the ray of light incident on the lens is parallel to the principal axis then after refraction it will pass through focus of the lens on the other side.
2. The ray of light if incident on lens through focus then after refraction it will go parallel to the principal axis.
3. A ray of light passing through optic center will go straight way on the same path.

Position, size and nature of images:

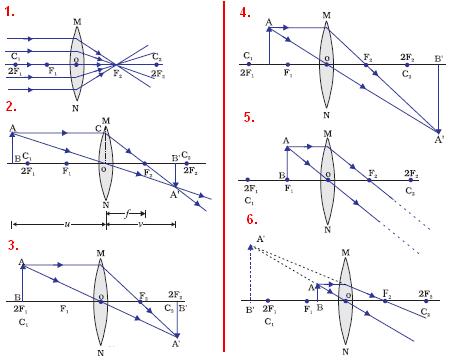
Position of object	Position of image	Nature of image	Size of image
At infinity	At Focus ‘F2’	Real & inverted	Point sized
At far from ‘2F1’	between ‘F2’ and ‘2F2’	’’	Diminished
At ‘2F1’	At ‘2F2’	’’	Same size as object
B/w ‘F1’ & ‘2F1’	Far from ‘2F2’	’’	Enlarged
At Focus ‘F1’	At infinity	’’	Highly enlarged
B/w ‘optical center’ & ‘F’	On the same side of the lens	Virtual & Erect	Enlarged

Image formation by concave lens:

There are certain rules which are followed in making ray diagrams of image formed by concave lens in the chapter of light reflection and refraction for class 10. They are:

1. When incident ray of light is parallel to the principal axis appear to diverge from a single point i.e focus on the same side of the lens.
2. When incident ray of light appears to pass through the focus, after refraction it goes parallel to the principal axis.
3. When ray is incident on the optic center of the lens it will pass straight without any deviation.

Position, size and nature of images formed by concave lens:

Position of object	Position of image	Nature of image	Size of image
At infinity	At Focus ‘F1’	Virtual & Erect	Point sized
B/w optic center and infinity	between ‘F’ and ‘O’	’’	Diminished

Lens formula:

• \(\frac{1}{v} – \frac{1}{u} = \frac{1}{f}\)
• Where v is the image distance, u is the object distance and f is the focal length.

Magnification:

• m = \(\frac{h_i}{h_o} = \frac{v}{u}\)
• Where m is magnification of lens, h_i is height of image, h_o is height of object, v is the image distance and u is the object distance.

Power of lens:

• The ability of lens to converge or diverge incident ray depends upon its focal length.
• The reciprocal of focal length (in meter) is said to be power of lens. Therefore, Power of the lens = p = \(\frac{1}{f}\)
• When focal length is measured in meter then its power has a unit ‘dioptre’. Also, it is its SI unit.
• The unit diopter is denoted by ‘D’.
• 1 dioptre may be defined as the power of lens when it has a focal length of 1 meter.
• Power of a lens is inversely proportional to thickness of the lens.
• Power of convex lens is positive whereas power of concave lens is negative.
• The power of combination of n number of lenses are P = P₁ + P₂ + P₃ + P₄ …….. + P_n.

In this article, all the topics related to light reflection and refraction are covered to the most extent. 

To Practice Questions and answers related to this chapter please Click here  Q/A on Light

Also read,
Life processes
Human respiratory system	Nutrition in animals
Control and coordination	Human Eye and colourful world
How do organisms reproduce?	Control and coordination
Heredity and evolution